MODELACIÓN DE SISTEMAS

TIPOS DE FUNCIONES

Función Escalón.

Una función escalonada es aquella función definida a trozos que en cualquier intervalo finito [a, b] en que esté definida tiene un número finito de discontinuidades c1 < c2 < ... < cn, y en cada intervalo abierto (ck, ck+1) es constante, teniendo discontinuidades de salto en los puntos ck.


En ingeniería es común encontrar funciones que corresponden a estados de sí o no, o bien activo o inactivo. Por ejemplo, una fuerza externa que actúa sobre un sistema mecánico o una tensión eléctrica aplicada a un circuito, puede tener que suspenderse después de cierto tiempo. Para tratar de forma efectiva con estas funciones discontinuas conviene introducir una función especial llamada función escalón unitario.
CARACTERÍSTICAS
Una función escalonada es aquella cuya gráfica tiene la forma de una escalera que pueden ascender o descender al ser dibujadas. El ejemplo más común de función escalonada es la función parte entera, Función escalón de Heaviside o función escalón unitario, y la función signo.
La composición de cualquier función escalonada s(x) y una función cualquiera f(x) da por resultado una función escalonada g(x) = f(s(x)), siempre que f(x) esté definida para cualquier valor de x en el rango de s(x).
Evidentemente, la derivada de una función escalonada es 0 en cualquier punto en que se halle definida. No puede definirse en los puntos en que hay discontinuidades.

Función Rampa

La función rampa es una función elemental real de un sólo argumento, continua y diferenciable en todo su dominio excepto en un punto (inicio de la rama) fácilmente computable a partir de la función mínimo o la función valor absoluto.
Las principales aplicaciones prácticas de esta función se dan en ingeniería (procesamiento digital, de señales, plasticidad, etc.). El término "función rampa" se debe a la forma de su representación gráfica.

La función rampa (denotada de diferentes maneras en la literatura científica:

Y que se define de esta forma:

Puede definirse de diferentes maneras equivalentes:

  

(en términos de la función valor absoluto) 

(en términos de la función máximo) 

(en términos de la función unitaria de Heaviside) 

Algunas formas menos elementales de definirla son: 

 

(primitiva de la función unitaria de Heaviside) 

(producto de convolución)

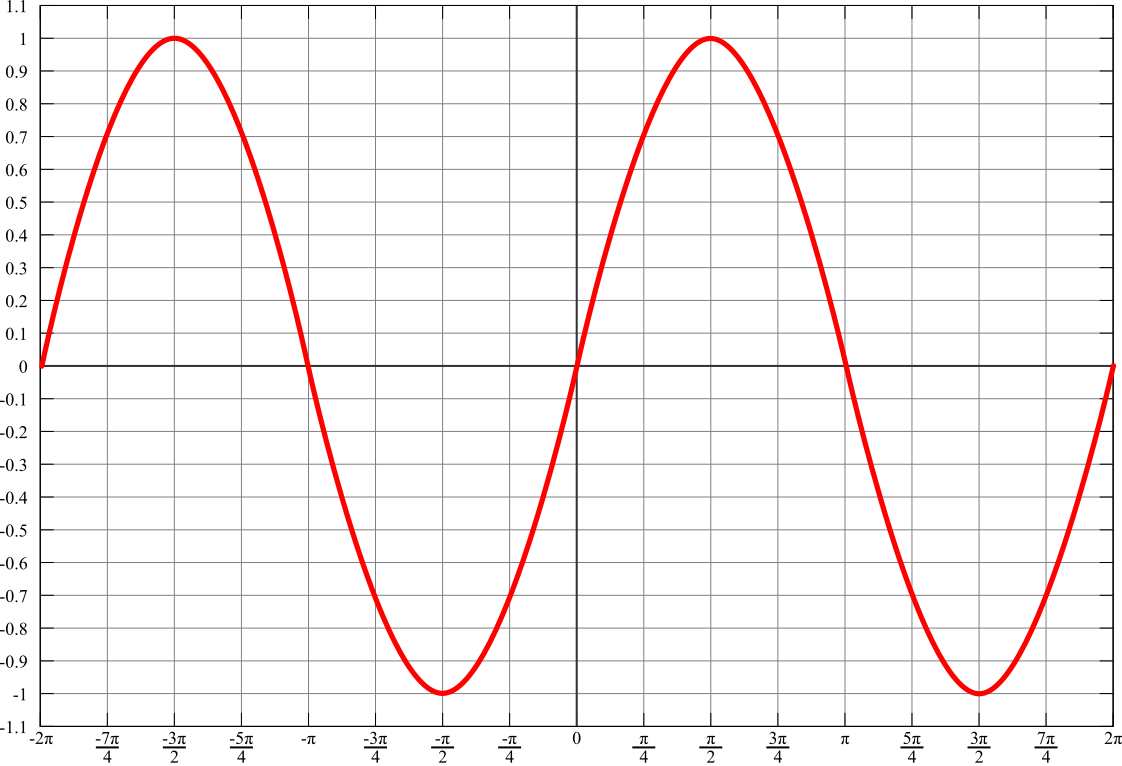
Función Senoidal

En matemáticas se denomina sinusoide o senoide a la curva que representa gráficamente la función seno y también a dicha función en sí. Es una curva que describe una oscilación repetitiva y suave.

Su forma más básica en función del tiempo (t) es:

La senoide es importante en física debido al hecho descrito por el teorema de Fourier que dice que toda onda, cualquiera que se sea su forma, puede expresarse de manera única como superposición (suma) de ondas sinosuidales de longitudes de onda y amplitudes definidas.Por este motivo se usa esta función para representar tanto a las ondas sonoras como las de la corriente alterna.

CARACTERÍSTICAS

Período (T) en una sinusoide

Es el menor conjunto de valores de que corresponden a un ciclo completo de valores de la función; en este sentido toda función de una variable que repite sus valores en un ciclo completo es una función periódica, seno o no sinusoidal.

En las gráficas de las funciones seno-coseno el período es .

Amplitud (A) en una sinusoide

Es el máximo alejamiento en el valor absoluto de la curva medida desde el eje x.

Desde un punto de vista más técnico, la amplitud de la sinusoide es la norma del supremo de la sinusoide:

Fase inicial (φ) en una sinusoide

La fase da una idea del desplazamiento horizontal de la sinusoide. Si dos sinusoides tienen la misma frecuencia e igual fase, se dice que están en fase.

Si dos sinusoides tienen la misma frecuencia y distinta fase, se dice que están en desfase, y una de las sinusoides está adelantada o atrasada con respecto de la otra.

Carece de sentido comparar la fase de dos sinusoides con distinta frecuencia, puesto que éstas entran en fase y en desfase periódicamente.

Función Impulso.

Algunos sistemas mecánicos suelen estar sometidos a una fuerza externa (o a una tensión eléctrica en el caso de los circuitos eléctricos) de gran magnitud, que solamente actúa durante un tiempo muy corto. Por ejemplo, una descarga eléctrica podría caer sobre el ala vibrante de un avión; a un cuerpo sujeto a un resorte podría dársela un fuerte golpe con un martillo, una pelota (de béisbol, de golf o de tenis) inicialmente en reposo, podría ser enviada velozmente por los aires al ser golpeada con violencia con un objeto como una bat de béisbol, un bastón de golf o una raqueta de tenis. La función impulso unitario puede servir como un modelo para tal fuerza.

¿PARA QUE SIRVEN LOS TEOREMAS DE LA TRANSFORMADA DE LAPLACE?

La Transformada de Laplace es una técnica Matemática que forma parte de ciertas transformadas integrales como la transformada de Fourier, la transformada de Hilbert, y la transformada de Mellin entre otras. Estas transformadas están definidas por medio de una integral impropia y cambian una función en una variable de entrada en otra función en otra variable. La transformada de Laplace puede ser usada para resolver Ecuaciones Diferenciales Lineales y Ecuaciones Integrales. Aunque se pueden resolver algún tipo de ED con coeficientes variables, en general se aplica a problemas con coeficientes constantes. Un requisito adicional es el conocimiento de las condiciones iniciales a la misma ED. Su mayor ventaja sale a relucir cuando la función en la variable independiente que aparece en la ED es una función seccionada. 

Cuando se resuelven ED usando la técnica de la transformada, se cambia una ecuación diferencial en un problema algebraico. La metodología consiste en aplicar la transformada a la ED y posteriormente usar las propiedades de la transformada. El problema de ahora consiste en encontrar una función en la variable independiente tenga una cierta expresión como transformada.

Definición de la Transformada Inversa

La transforma inversa de una función de s de la forma F(s-a) se puede resolver a través del uso del primer teorema de traslación de la transformada de laplace.

La inversa será igual a e^at por la inversa de F(s) que se forma tras cambiar s-a por s.

En muchos casos esta técnica es un mejor alternativa frente al uso de fracciones parciales ya que no todas las funciones racionales nos permiten factorizar el denominador cuando este es una función cuadrática. Es por ello que se hace necesario hacer uso de la completación del trinomio cuadrado perfecto.

TIPOS DE SISTEMAS DE CONTROL

1.Sistema de lazo abierto.
Dentro de la ingeniería de sistemas, un sistema de control es un conjunto de dispositivos encargados de administrar, ordenar, dirigir o regular el comportamiento de otro sistema, con el fin de reducir las probabilidades de fallo y obtener los resultados deseados. Por lo general, se usan sistemas de control industriales en procesos de producción industriales para controlar equipos o maquinas.

2. Sistema de lazo cerrado.

Los sistemas de control en lazo cerrado, son aquellos en los que existe una re alimentación de la señal de salida o, dicho de otra forma, aquellos en los que la señal de salida tiene efecto sobre la acción de control.

3. Control de velocidad.
El control de velocidad, también conocido como regulador de velocidad, es un sistema que controla de forma automática el factor de movimiento de un vehículo de motor. El conductor configura la velocidad y el sistema controlará la válvula de aceleración o throttle del vehículo para mantener la velocidad de forma constante.

4. Control de un robot.
El controlador es el componente del robot que procesa la información captada por los sensores, y según las instrucciones del programa que almacena, regula el movimiento de los motores u otros dispositivos de salida.


Todos los robots son sistemas, es decir, constan de componentes que forman un todo. El sistema robótico se puede analizar de lo general a lo particular utilizando el análisis sistemático. El primer paso es considerar al sistema como una "caja negra", no sabemos qué hay en su interior, pero podemos identificar la entrada y salida del sistema. La entrada genuina al robot está constituida por las órdenes humanas; la salida está formada por diversos tipos de trabajo realizado automáticamente.

5. Control de temperatura.

Un control de temperatura es un instrumento el cual ayuda a mantener un valor deseado con la menor variación posible, también son conocidos como controladores de temperatura o piró-metros.
El objetivo de un sistema de control de temperatura es mejorar el confort del usuario y al mismo tiempo incurrir en un ahorro energético; debemos señalar que o existe un solo tipo, aunque hasta hace un par de años atrás este sistema era único

6. Control Empresarial
El Control Empresarial es un Proceso Administrativo muy ligado con la plantación, el control es la fase a través del cual se evalúan los resultados obtenidos en relación con lo planeado, a fin de corregir desviaciones y errores para mejorar continuamente.
Podemos definirlo como: La función que permite la supervisión y comparación de los resultados obtenidos contra los resultados esperados originalmente, asegurando además que la acción dirigida se esté llevando a cabo de acuerdo con los planes de la organización y dentro de los límites de la estructura organizacional.

VENTAJAS DEL SISTEMA DE CONTROL DE LAZO ABIERTO

1. Simple construcción y fácil mantenimiento.
2. Menos costoso que un correspondiente sistema de lazo cerrado.
3. No hay problema de estabilidad.
4. Conviene cuando salidas son duras o difíciles de medir o económicamente es no viable.

DESVENTAJAS

1.Perturbaciones y cambios en la calibración causan errores, y la salida puede ser diferente de aquella deseada.

2. Para mantener la calidad requerida en la salida, es necesario recalibrar de vez en cuando.

EJEMPLOS DE LAZO ABIERTO EN LOS HOGARES

1. MICROONDAS

En este caso la variable controlada debería ser la cocción del alimento que introducimos, la variable de entrada sería el tiempo el cual lo ingresamos a través del tablero de control que vendría a ser parte de los componentes del sistema de control. Como sabemos intuitivamente nosotros digitamos el tiempo de cocción este puede ser o no el correcto sin embargo el microondas como tal no mide ni se retroalimenta de esta variable, en caso de no ser suficiente el tiempo nosotros volvemos a meter otro tiempo cerrando nosotros el lazo, pero en si el microondas es un sistema de control a lazo abierto

2. SINTONIZAR UN CANAL EN LA TV
En muchas ocasiones se va la señal en ciertos canales y lo más común es que solemos mover la antena para que sintonice correctamente, bueno el sistema de la TV no tiene retroalimentación ya que como sabemos si no tiene señal simplemente la salida que sería la calidad de la imágenes mala, automáticamente no se gira o regula la antena por sí misma.

3. CONTROL DEL VOLUMEN EN EL AUTO
La variable controlada sería el nivel de salida de los parlantes, el cual como sabemos en el auto no es censado ni actúa como alimentación en el control, el sistema de control sería el sistema de audio en el cual como componente se incluye la perilla que nos permite regular la salida.